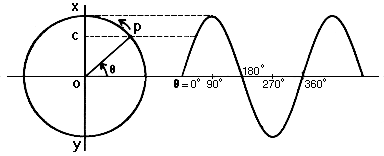
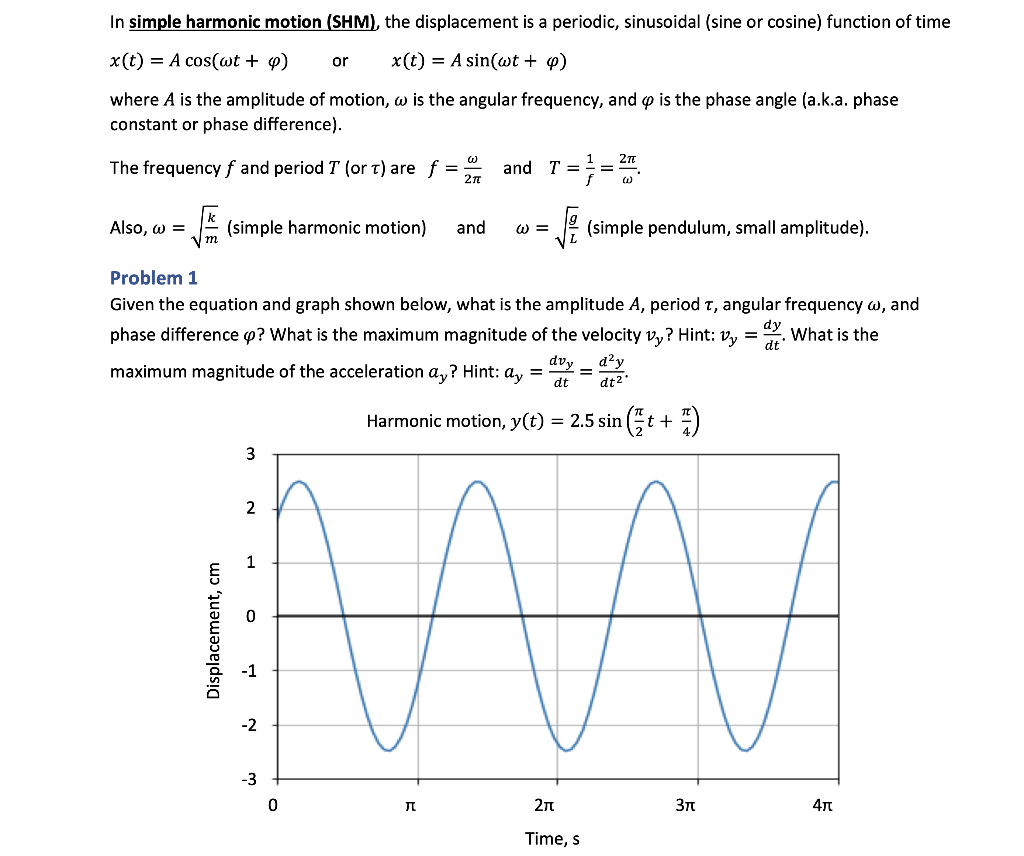
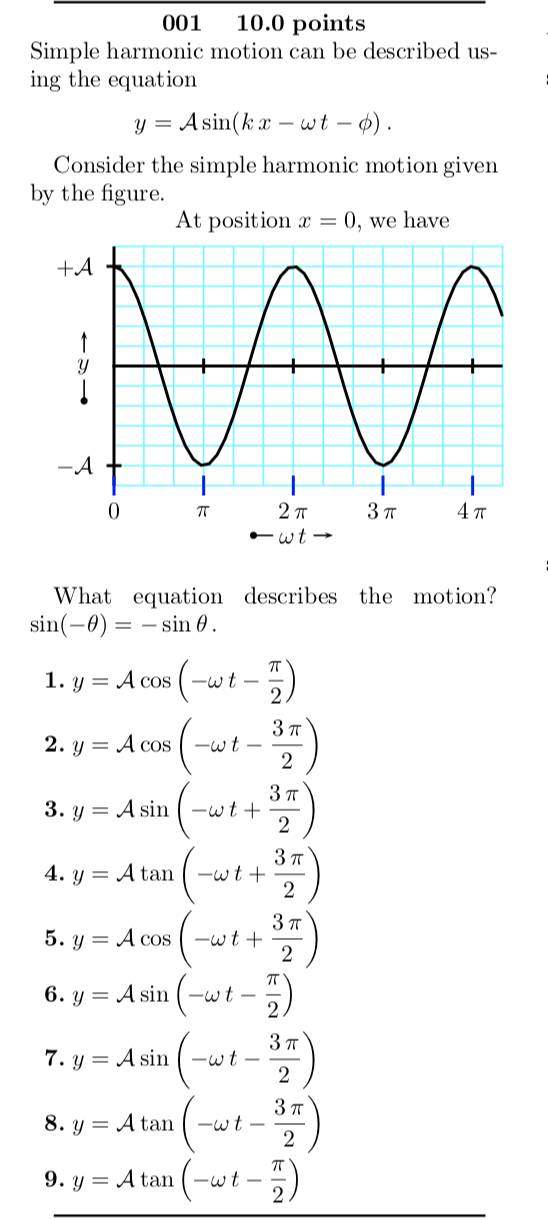
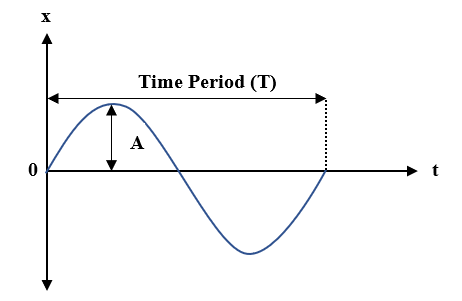
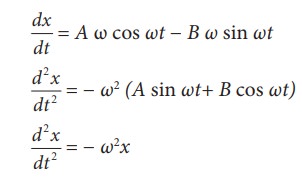The displacement of a particle executing simple harmonic motion is given by y=A(0)+A sin omegat+B cos omegat. Then the amplitude of its oscillation is given by
Simple Harmonic Motion (Sine and Cosine Models) Ex 1 - YouTube
Simple_Harmonic_Motion
The corresponding harmonic circular motion of a simple harmonic... | Download Scientific Diagram
Solved In simple harmonic motion (SHM), the displacement is | Chegg.com
Solved 001 10.0 points Simple harmonic motion can be | Chegg.com
Solved Example Problems for Simple Harmonic Motion (SHM) - Oscillations | Physics
The Harmonic Oscillator - ppt download
Simple Harmonic Motion
The displacement equation of a simple harmonic oscillator is given by y=A sin omegat-Bcos omegat The amplitude of the oscillator will be
The amplitude of SHM $y= 2(\\sin{5 \\pi t}+ \\sqrt{2} \\cos{\\pi t})$ is
Mechanics - Hooke's Law, Newton's Second Law, Simple Harmonic Motion, and Resonance | Britannica
the amplitude of the simple harmonic motion is Y=(3 sin omega t+4 cos omega t)m
SOLVED: "Verify this equation represent simple harmonic motion or not? (i) x = A sin ωt + B cos ωt"
Simple Harmonic Motion AP Physics C. Simple Harmonic Motion What is it? Any periodic motion that can be modeled with a sin or cosine wave function. - ppt download
Solution Set - Simple Harmonic Motion - Physics 107
the displacement of a harmonic oscillator is given by X equals to Alpha Sin Omega T + b cos Omega T them Period of the oscillator is given by
classical mechanics - Why is this SHM derivation the way it is? - Physics Stack Exchange
Lesson 47 Simple Harmonic Motion and Sum of Trig Functions - YouTube
